Distribución de Poisson

/ Costado ingeniero / Por / Estadistica

La Distribución de Poisson es una distribución de probabilidad discreta que se utiliza en negocios y otros campos para modelar la probabilidad de que ocurra un número específico de eventos en un intervalo fijo de tiempo o espacio, asumiendo que estos eventos ocurren con una frecuencia media conocida (\lambda) y de manera independiente entre sí.

Fórmula

La distribución se basa en la siguiente fórmula:

    \[ \boxed{P(X=k) = \frac{\lambda^k e^{-\lambda}}{k!}} \]

P(X=k): Probabilidad de que ocurran exactamente k eventos.

\lambda (lambda): Tasa promedio de ocurrencia.

e: Base del logaritmo natural.

k!: Factorial de k.

🎯 Aplicaciones de la Distribución de Poisson en Negocios

La estadística de Poisson es valiosa para la toma de decisiones informadas, especialmente en áreas donde se gestionan tasas de llegada, fallos o demanda:

  • Gestión de Inventario y Demanda:
    • Estimar la demanda de un producto para determinar los niveles de stock óptimos y evitar excesos o roturas.
    • Predecir el número de pedidos que se recibirán en un período de tiempo.
  • Servicio al Cliente y Operaciones:
    • Modelar el número de llamadas recibidas en un call center por hora para dimensionar el personal de manera eficiente.
    • Estimar la llegada de clientes a una tienda, banco o restaurante para optimizar los horarios y el flujo de servicio.
    • Predecir el número de fallos de máquinas o componentes en un período de tiempo para planificar el mantenimiento preventivo.
  • Calidad y Control de Procesos:
    • Contar el número de defectos por unidad de área o volumen (por ejemplo, defectos en metros cuadrados de tejido o en páginas de un libro).
  • Seguros y Finanzas:
    • Modelar el número de reclamaciones que una aseguradora recibe en un período dado.
    • Predecir el número de transacciones o fallos en sistemas financieros.

Ejemplo de Distribución de Poisson en un Restaurante

Escenario: Llegada de Clientes al Almuerzo

Una cadena de restaurantes de comida rápida quiere optimizar la dotación de personal en la caja durante la hora pico del almuerzo.

  • Variable Aleatoria (X): El número de clientes que llegan a la caja de pedidos en un lapso de 10 minutos.
  • Contexto: Los gerentes han observado que el número promedio de clientes que llegan cada 10 minutos durante el pico es de 4 clientes.
  • Parámetro (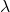\lambda): La tasa promedio de ocurrencia (clientes por 10 minutos), \lambda = 4.

Cálculo de Probabilidad

Usaremos la fórmula de la distribución de Poisson para calcular la probabilidad de un evento específico:

    \[P(X=k) = \frac{e^{-\lambda} \lambda^k}{k!}\]

Donde:

  • P(X=k) es la probabilidad de que ocurran exactamente k eventos.
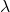  • \lambda es el promedio de eventos (4).
  • e es la base del logaritmo natural (\approx 2.71828).
  • k! es el factorial de k.

Pregunta de Negocio

¿Cuál es la probabilidad de que lleguen exactamente 6 clientes a la caja en los próximos 10 minutos? (Para decidir si se necesita una segunda caja abierta).

  • k = 6
  • \lambda = 4

Solución

    \[P(X=6) = \frac{e^{-4} 4^6}{6!} = \frac{(0.0183) \cdot (4096)}{720} \approx 0.1042\]

Conclusión y Aplicación

La probabilidad de que lleguen exactamente 6 clientes en ese período de 10 minutos es de aproximadamente 10.42%.

Esta información le permite al gerente tomar decisiones informadas:

  • Dotación de Personal: Si la probabilidad de 6 o más clientes es alta, justifica mantener una segunda caja abierta.
  • Gestión de Inventario: Permite predecir la demanda de ingredientes frescos o platos ya preparados.
  • Tiempo de Espera: Ayuda a establecer los niveles de servicio y a mitigar las colas excesivas.

En resumen, la distribución de Poisson permite al negocio gastronómico predecir la demanda y optimizar la eficiencia operativa basándose en la tasa promedio de llegadas.

Novedades